假设我们要判断ABABAC （pat） 是否为 ABABADEF (str) 的子串，一种显而易见的方式是，从str的第 0 个字符开始，逐一与 pat匹配。若匹配失败，则再从 str 的第 1 个字符开始，逐一与pat匹配。以此类推，直至匹配成功或者尝试到str的最后一个字符。

这种方式写起来很简单方便，但是仔细想想，匹配失败后直接从头开始是不是会做一些无用功？

一个例子

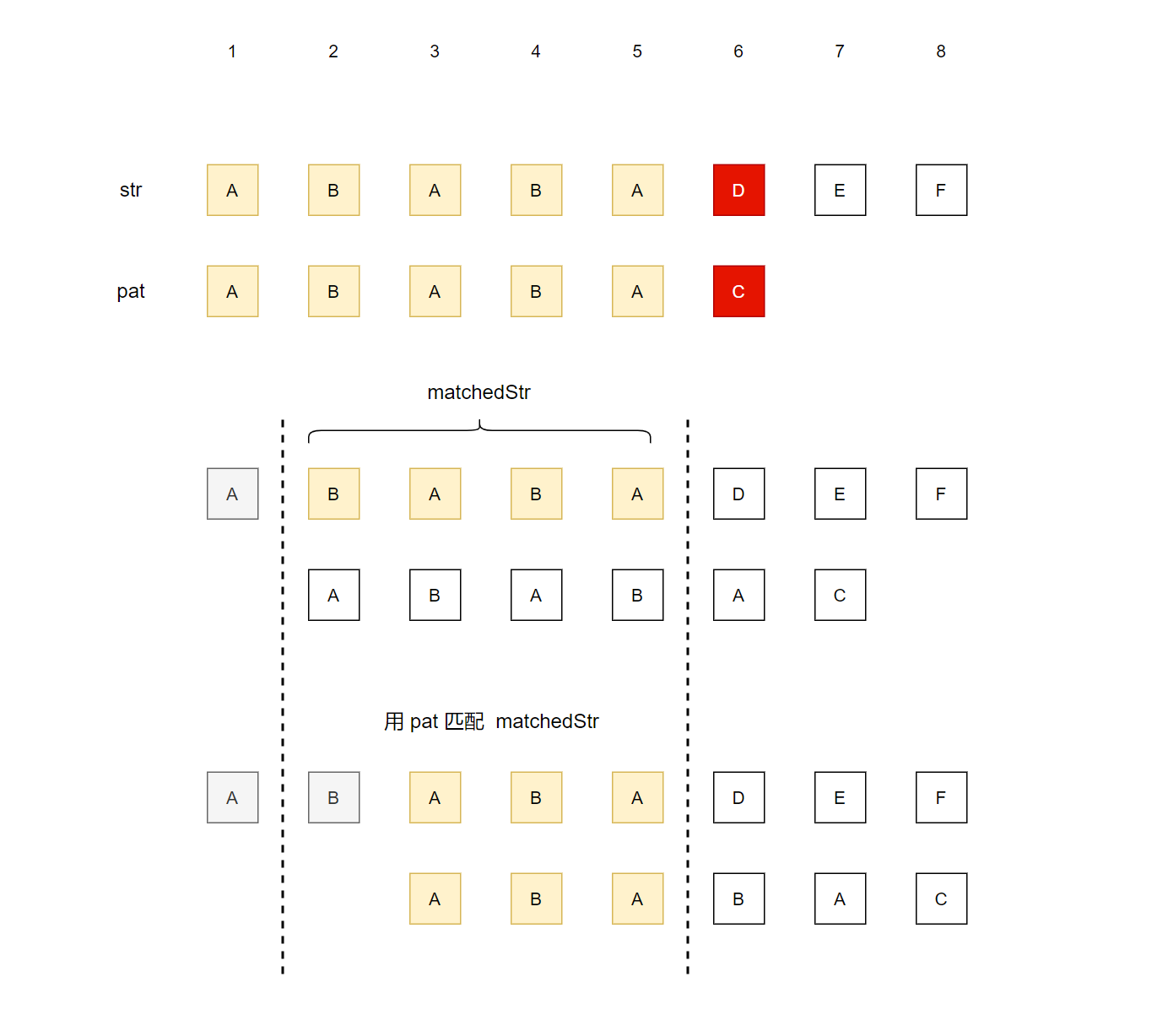
下图展示的是ABABADEF (str) 匹配 ABABAC （pat）的过程，前5个字符顺利匹配成功，但是在第6个字符匹配失败。

那么我们就从str的第 2个字符重新开始匹配，发现又匹配失败了。接着从str的第 3个字符开始匹配，然后我们会发现，咦，ABA又出现了！我们把 BABA记为matchedStr，表示除了第1个字符外，在第1次匹配中成功匹配的。第1次匹配失败后，其实问题就转化成了 在matchedStr中找pat的前缀。

当然，我们可以暴力地从头开始逐个匹配，但是有没有更好的方式呢？matchedStr 其实是 pat 的子串呀，对于任意的matchedStr ，我们其实可以事先算出其在 pat 中的前缀。那么不管在str的什么地方失败，我们都可以很快地找到从哪里开始重新匹配。

总结而言，思路是这样的：

  1. 匹配失败了，得到了 matchedStr
  2. 要重新开始匹配了，其实是在 matchedStr 里面找 pat 的前缀
  3. 既然matchedStr 是 pat 的子串，那么是不是可以提前计算出任意matchedStr的应对方案，并且与str无关？

怎么找前缀

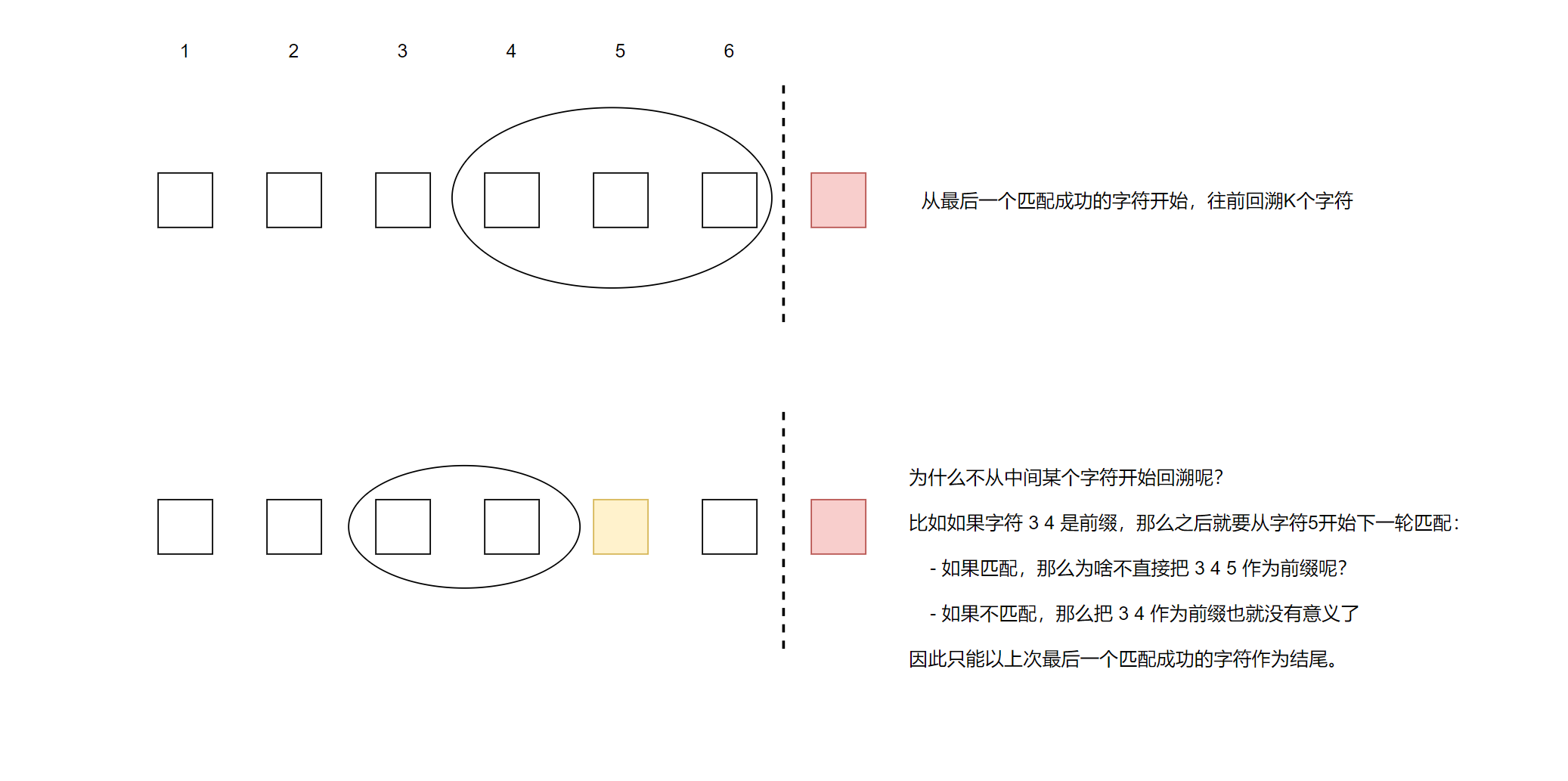
那么问题来了，怎么在 matchedStr 中找 pat 的前缀呢？首先我们得明确一点，找到的前缀必须是matchedStr的后缀。也就是：从最后一个匹配成功的字符开始，往前回溯k个字符，使其形成的子串可以作为 pat 的前缀。

为什么要从最后一个字符，而不是中间的某个字符呢？

以下图为例，如果字符 3 4 是前缀，那么之后就要从字符5开始下一轮匹配：

  • 如果匹配，那么为啥不直接把 3 4 5 作为前缀呢？
  • 如果不匹配，那么把 3 4 作为前缀也就没有意义了

因此我们不如贪心一点，直接匹配到 matchedStr 的最后一个字符，一步到位。

restart point

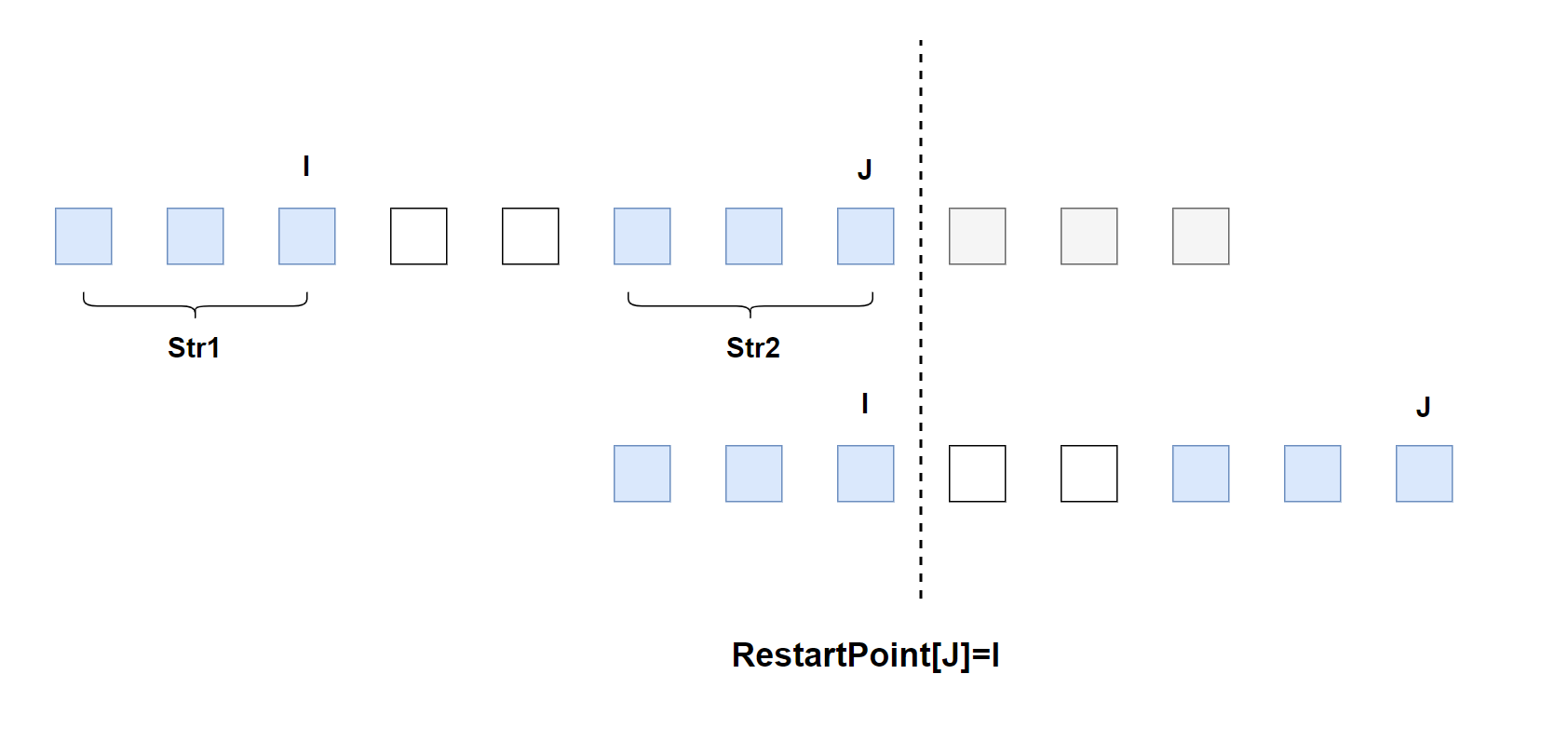
找到前缀后，比如以字符J结尾的Str2 找到了与之对应的前缀Str1，Str1 的最后一个字符index是I，那么我们将从I处重新往后匹配。此时，我们把I 称为 J的 restart point。

只要能算出任意的J对应的I，那么就能快速从错误中恢复了。

转换成 DFA

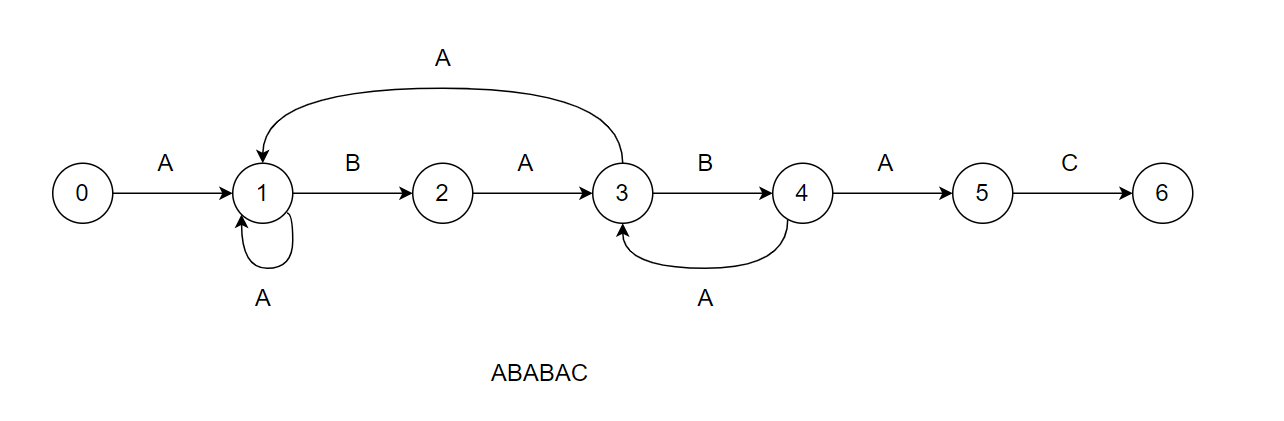
由于有了 restart point的存在，pat 中的每个字符都可以在匹配失败后跳转到 restart point 进行“续命”；而 restart point 的下一个字符又与其自身的下一个字符可能会不相同，因此pat 中的每个字符都有多种“去向”。这种场景用 DFA 来表示比较方便。

还是以 ABABAC 为例，我们把匹配过程以 DFA 的形式展示出来。匹配一个字符，相当于一次状态转移。 ABABAC的第二个B的 restart point 是第一个B， 第一个B能通过匹配A转移到状态3，那么状态4也可以通过匹配A转移到状态3。

（遇到其它没有画出来的字符，直接转移到状态0）

构建 DFA

给定任意pat，怎么构建上述的 DFA呢？记dfa[i][c]表示状态i遇到字符c后可以转移到的新状态。比如对于ABABAC，有dfa[1]['A']=1，dfa[1]['B']=2，dfa[1]['C']=0。

又记RP[i]为字符i对应的restart point 那么有 RP[i + 1] = RP[i] + pat[i]，+ pat[i]表示在RP[i]后，紧接着匹配一个字符pat[i]。比如对于ABABAC，在BABA中找pat的前缀时，先要在BAB找，也就是先要在BA中找，即：

BABA -> BAB -> BA -> A，也就是 RP[4] = RP[3] + 'A' = RP[2] + 'B' = RP[1] + 'A'

那么就有 dfa[i][c] = dfa[X][c]，其中X为i的restart point，且有 Xi+1 = dfa[Xi][c] （没有 restart point的话，就会回到状态0重新开始）。因此有DFA的构建代码：

int[][] dfa = new int[pat.length()][26];

int X = 0;
int state = 1;
dfa[0][pat.charAt(0) - 'a'] = 1;

for (int i = 1; i < pat.length(); i++) {
    for (int c = 0; c < 26; c++) {
        dfa[state][c] = dfa[X][c];
    }

    int c = pat.charAt(i) - 'a';
    dfa[state][c] = ++state;
    X = dfa[X][c];
}

开始匹配

构建完DFA后，就可以开始匹配字符串str了。依次遍历str的各个字符，在DFA中进行状态转移，若转移到最后一个 state （== pat.length()）则表示匹配成功，否则表示匹配失败。

state = 0;
for (int i = 0; i < str.length(); i++) {
    state = dfa[state][str.charAt(i) - 'a'];
    if (state == pat.length()) {
        return i - pat.length() + 1;
    }
}
return -1;

图片原始绘图文件见 KMP.drawio

可以在这里验证Leetcode 28

Ref: