-
-
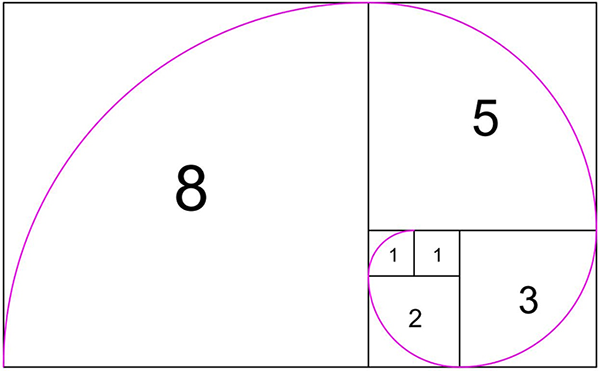
斐波拉契数列,即形如
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...,通项公式为An = An-1 + An-2的数列。那么怎么用递归的方式求出指定位置的斐波拉契数呢?
-

我们需要实现这样的一个
cache(key-value pair):- 取数据时,存在则取出,不存在则返回-1
- 存数据时,若该key已存在,则更新其value。若不存在,则插入之。插入时,若cache已满,则需要先删除一个元素。删除时,使用
LFU算法,将使用频率最低的元素删除;若有多个使用频率相同的元素,则对这些元素采用LRU算法,删除最久未使用的。
很显然,我们需要用
map来存储key-value pair。然后记录各个元素的使用频率,以及最近访问的次序。
-
拿到题目之后,最先想到的就是构建
NFA然后逐字符匹配。可以发现,整个题目的关键之处在于*的处理。首先画出*的状态图,如下: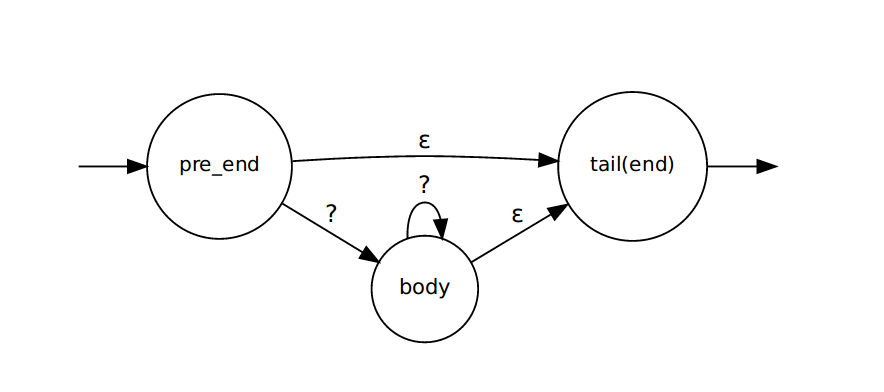
在
pre_end状态遇到了*,生成了入上图所示的状态转换,*的处理在tail(end)状态结束。算法如下:- 根据
pattern生成对应的NFA - 依次输入待匹配的字符,进行状态转换。转换时同步匹配多个分支,不使用回溯。也就是每次输入结束后可以有多个状态满足要求,参见Regular Expression Matching Can Be Simple And Fast
- 输入完所有字符后,检查当前停留的节点中是否有终止节点,有则匹配成功,反之不然。
- 根据
-
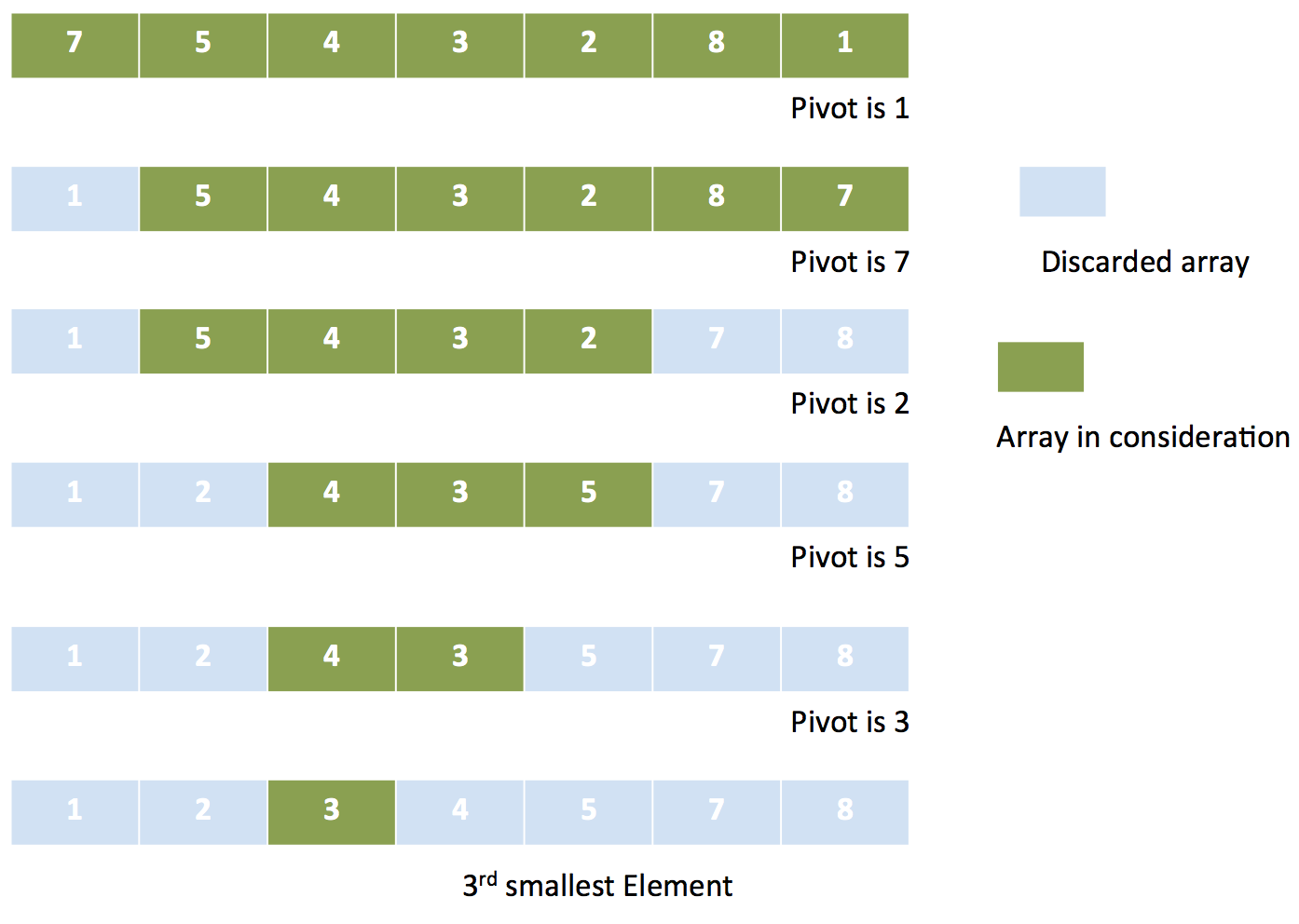
怎样从一个未排序数组中找出第K大的数?最简单的方法便是先将数组排序,然后便可取出第K大的数了。显然,此方法有点“大材小用”,其实没必要将数组所有元素排序,只需要取出指定的元素即可。那么可不可以改进一下现有的排序算法,使之无需排序整个数组,就能找到第K大的元素呢?
我们可以将快速排序改进一下:每次基于
pivot将元素分为大小两类后,舍弃目标元素不会存在于其中的那个部分。具体算法如下:- 选定一个
pivot,将其余元素分成小于或等于pivot,以及大于pivot两类,分别记为smaller与greater - 记
len( greater ∪ pivot ) = counter: - 若
counter = K,表明pivot即为第K大的元素 - 若
counter > K,表明该元素在greater部分,那么smaller部分就可以舍弃无需考虑了;回到步骤1,在greater中再次寻找第K大的元素 - 若
counter < K,表明该元素在smaller部分,那么greater部分就可以舍弃;并在smaller中寻找第K-counter大的元素
- 选定一个
-

选择排序,即依次在待排序列表中找出最小者,放置到待排序列表最左端。初始时,待排序列表为整个列表。