
我们需要实现这样的一个cache(key-value pair):
- 取数据时,存在则取出,不存在则返回-1
- 存数据时,若该key已存在,则更新其value。若不存在,则插入之。插入时,若cache已满,则需要先删除一个元素。删除时,使用
LFU算法,将使用频率最低的元素删除;若有多个使用频率相同的元素,则对这些元素采用LRU算法,删除最久未使用的。
很显然,我们需要用map来存储key-value pair。然后记录各个元素的使用频率,以及最近访问的次序。主要有下面三个操作:
- 获取数据:从cache中获取指定Key对应的元素,同时更新使用频率以及最近访问的次序。
- 插入数据:将新元素插入到cache
- 删除元素:当cache已满时,按照
LFU-LRU算法删除一个元素
只记录频率
若只考虑记录使用频率,我们可以使用最小堆来实现:
使用两个map,一个存key-value pair,记为map1;一个存key-node pair,记为map2。node中存频率。
- 获取数据:从map1取出数据用来返回,从map2取出node,将频率增加之后,调整以其为根的子树,使其满足最小堆的性质。
- 插入数据:将数据存到map1,生成一个新node,频率为0,将其插入最小堆。
- 删除数据:先从map1中删除堆顶元素对应的数据,然后从删除堆顶元素,并调整结构即可。
只记录最近访问顺序
同样需要两个map,只是此时的node是双向链表中的node。维护一个双向链表,记录首尾指针
- 获取数据:从map1中获取数据;然后将双向链表中对应的node移到链表最前面。由于是双向链表,整个过程只需要更改左右指针即可。
- 插入数据:插入数据到map1;将新生成的node放置到链表最前面
- 删除数据:从map1中删除链表末尾的node对应的数据;然后将该node从链表中删除。
结合频率与访问顺序
可以发现,使用堆来记录访问频率时,上述三个操作中,每个操作的算法复杂度都是O(logn);而用双向链表记录访问次序时,每个操作的算法复杂度都是O(1)。
从堆中找到频率最小者后,还需要从双向链表中找出对应频率的node,才能根据其在链表中的相对次序移除最近未使用者。计算相对次序时,无异于遍历整个链表了,本来O(1)的算法会降为O(n)了。怎么将二者结合起来呢?
既然每个频率都要找出一个相对而言的LRU List,我们为何不弃用最小堆,直接记录频率与LRU List的关系呢?
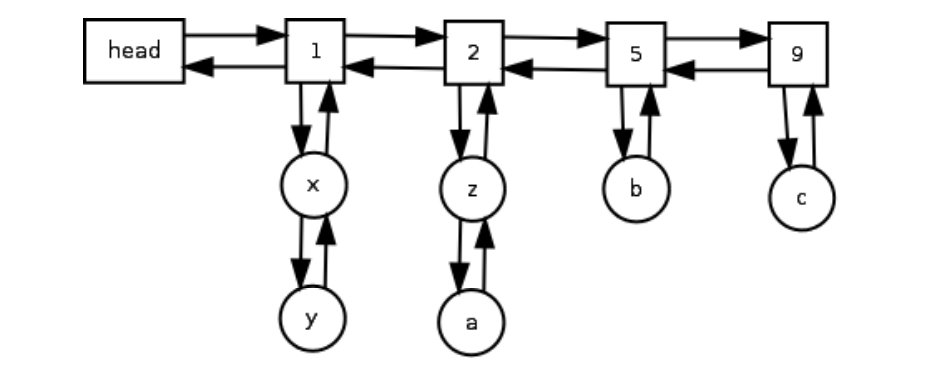
如图所示,将频率依次用双向链表连接,每个频率都有一个对应的LRU List与之关联。我们仍要维护两个map。map1存储key-node pair,node都要记录其对应的值以及频率;map2存frequency-node,此node要记录其对应的LRU List
- 获取数据:从map1中获取数据node.value,此时,node的频率要增加,因此要通过map2[node.freq+1]找到对应的频率
LRU List。如果不存在,则创建LRU List。存在则将node放到队首。 - 插入数据:先找到频率链的队首,若队首频率为0,则将新建的node加入
LRU List的队首,否则要新建一个频率为0的。 - 删除数据:删除频率链队首对应的
LRU List队尾元素
三种操作算法复杂度都是O(1)。
Reference: An O(1) algorithm for implementing the LFU cache eviction scheme
Code: https://github.com/YieldNull/leetcode/blob/master/460_LFU_Cache.java