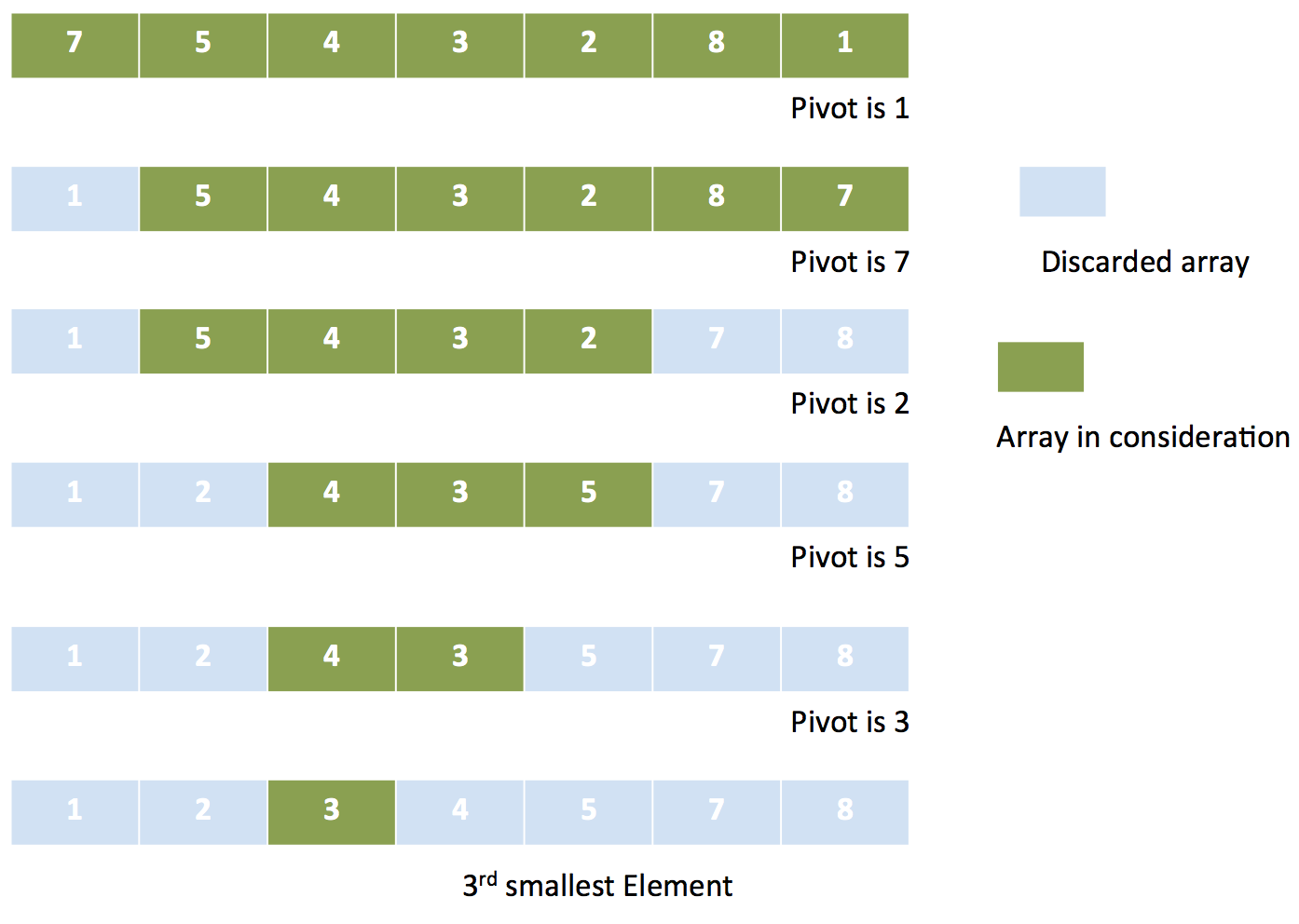
怎样从一个未排序数组中找出第K大的数?最简单的方法便是先将数组排序,然后便可取出第K大的数了。显然,此方法有点“大材小用”,其实没必要将数组所有元素排序,只需要取出指定的元素即可。那么可不可以改进一下现有的排序算法,使之无需排序整个数组,就能找到第K大的元素呢?
我们可以将快速排序改进一下:每次基于pivot将元素分为大小两类后,舍弃目标元素不会存在于其中的那个部分。具体算法如下:
- 选定一个
pivot,将其余元素分成小于或等于pivot,以及大于pivot两类,分别记为smaller与greater - 记
len( greater ∪ pivot ) = counter: - 若
counter = K,表明pivot即为第K大的元素 - 若
counter > K,表明该元素在greater部分,那么smaller部分就可以舍弃无需考虑了;回到步骤1,在greater中再次寻找第K大的元素 - 若
counter < K,表明该元素在smaller部分,那么greater部分就可以舍弃;并在smaller中寻找第K-counter大的元素
用代码描述如下:
def recursion(nums, k):
pivot = nums[0]
smaller = [x for x in nums[1:] if x <= pivot]
greater = [x for x in nums[1:] if x > pivot]
counter = len(greater) + 1
if counter == k:
return pivot
elif counter > k:
return recursion(greater, k)
else:
return recursion(smaller, k - counter)
上述代码会残生额外的空间复杂度,其实可以使用更合理的in-place方法,无需使用额外的空间将元素分为大小两类:
def inplace(nums, k):
return inplace_recursion(nums, 0, len(nums) - 1, k)
def inplace_recursion(nums, left, right, k):
pivot = nums[left]
p_pivot = _inplace_partition(nums, left, right)
counter = p_pivot - left + 1
if counter == k:
return pivot
elif counter > k:
return inplace_recursion(nums, left, p_pivot - 1, k)
else:
return inplace_recursion(nums, p_pivot + 1, right, k - counter)
我们需要一种原地分割方法_inplace_partition(nums, left, right),在给定区间[left,right]内,将较大部分放在pivot左侧,将较小部分放在右侧,然后返回pivot位置,这样就成功地将元素分类了。与快速排序相同,只需要维护一头一尾两个指针,依次将指针向中间移动:
def _inplace_partition(nums, left, right):
pivot = nums[left]
p_left = left
p_right = right + 1
while p_left < p_right:
p_left += 1
p_right -= 1
while p_left <= right and nums[p_left] > pivot:
p_left += 1
while p_right >= left and nums[p_right] < pivot:
p_right -= 1
if p_left < p_right:
nums[p_left], nums[p_right] = nums[p_right], nums[p_left]
nums[left], nums[p_right] = nums[p_right], nums[left] # place pivot in the middle
return p_right
(完)