1. NFA无回溯匹配
拿到题目之后,最先想到的就是构建NFA然后逐字符匹配。可以发现,整个题目的关键之处在于*的处理。首先画出*的状态图,如下:
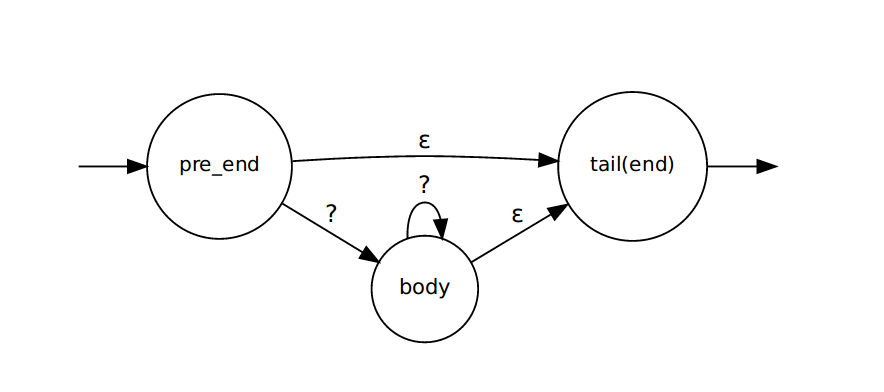
在pre_end状态遇到了*,生成了如上图所示的状态转换,*的处理在tail(end)状态结束。算法如下:
- 根据
pattern生成对应的NFA - 依次输入待匹配的字符,进行状态转换。转换时同步匹配多个分支,不使用回溯。也就是每次输入结束后可以有多个状态满足要求,参见Regular Expression Matching Can Be Simple And Fast
- 输入完所有字符后,检查当前停留的节点中是否有终止节点,有则匹配成功,反之不然。
1.1 NFA的构建
NFA可以由节点与箭头表示,每个节点需要记录以其为起点的箭头,箭头表示由某个字符引发的状态转换,指向目的节点:
static class Node {
static final char EMPTY_ARROW = 0; // ε
int index; // for remain steps estimation
Map<Character, Node> outArrows = new HashMap<>();
Node(int index) {
this.index = index;
}
void addArrow(char chr, Node dest) {
outArrows.put(chr, dest);
}
}
只需要根据输入的pattern依次构建节点即可,需要记录开始节点用来开始匹配,记录终止节点用来检测是否匹配成功:
Node buildNFA(String pattern) {
Node start = new Node(0);
end = start;
for (int i = 0; i < pattern.length(); i++) {
char chr = pattern.charAt(i);
if (chr == '*') {
// reduce continuous '*' to single one
if (i - 1 >= 0 && pattern.charAt(i - 1) == '*') continue;
// do not increase wildcard index
Node body = new Node(end.index);
Node tail = new Node(end.index);
end.addArrow('?', body);
end.addArrow(Node.EMPTY_ARROW, tail);
body.addArrow('?', body);
body.addArrow(Node.EMPTY_ARROW, tail);
end = tail;
} else {
Node node = new Node(end.index + 1);
end.addArrow(chr, node);
end = node;
}
}
return start;
}
构建时,可以将连续的*缩减为一个,因为*******与*是等效的。观察上述代码可以注意到,每个Node都有一个与之关联的index值,这关系到匹配时的优化问题,暂且不表,下面会详述。
1.2 NFA的无回溯匹配
由于受到Regular Expression Matching Can Be Simple And Fast 一文的影响,选择了无回溯的匹配方式,将NFA中的各个分支同时进行匹配。比如在pre_end节点遇到*后,当前激活的节点便是pre_end与tail,待下一个节点输入后,同时从这两个节点进行状态转换。而不是先随机选一条路径,若无法达到终止节点,再回过来走另一条路径。
我们需要使用Set存储当前激活的节点,因为当pattern中由多个*时,由于body节点的存在自转换(待在原地),会导致通过不同的节点进行状态转换后,到达相同的节点。
转换算法如下:
Node end;
Set<Node> currentNodes = new HashSet<>();
public boolean isMatch(String str, String pattern) {
Node start = buildNFA(pattern);
addClosure(end.index, start);
for (int i = 0; i < str.length(); i++) {
char chr = str.charAt(i);
int remainSteps = str.length() - 1 - i;
Node[] currentCopy = currentNodes.toArray(new Node[currentNodes.size()]);
currentNodes.clear();
// step from current nodes
for (Node node : currentCopy) {
Node explicit = node.outArrows.get(chr);
Node wildcard = node.outArrows.get('?');
if (explicit != null) addClosure(remainSteps, explicit);
if (wildcard != null) addClosure(remainSteps, wildcard);
}
}
for (Node node : currentNodes) {
if (node == end) return true;
}
return false;
}
算法开始时,先求开始节点的闭包,然后将其中的节点设置为激活状态。接着依次输入字符,进行状态转换。整个NFA只对两种字符进行转换,其一为字母,其二为通配符?。转换后,同样要求出转换后状态的闭包。匹配整个字符串的过程中,会不断地更新其激活的当前节点。最后,等到所有输入字符串处理完毕,检查“当前节点”中是否存在终止节点,也就是是否存在合法路径,若有,则匹配成功。
1.3 匹配优化
可以在上面的匹配算法中发现如下代码int remainSteps = str.length() - 1 - i;,这是为优化做准备。由于匹配过程中存在多个正在尝试的路径,当遇到下面的测试用例时,最后会导致几乎所有节点都是激活状态。第一个*会源源不断地向前产生激活的a节点,这些节点会占用绝大多数的匹配时间,但是在匹配结束前不可能到达终点。
"aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
"*aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa*"
因此,在Node中记录其index,每次匹配字符时,计算剩下未输入的字符最多会使状态前进多少步,若该步数无法到达终点,也就不需要将相应的节点激活了。通过节点的index与终止节点的index进行比较,可以预估步数。在求闭包时剔除无用的节点
void addClosure(int remainSteps, Node node) {
Node emptyMove = node.outArrows.get(Node.EMPTY_ARROW);
if (end.index - node.index <= remainSteps){
currentNodes.add(node);
if (emptyMove != null) currentNodes.add(emptyMove);
}
}
在生成*对应节点时,body与tail使用相同的index。
2. 基于回溯的NFA
实践之后才发现,在本题的情况下,由于产生分支的情况过于简单,其实匹配时采用回溯的方式可以达到更高的效率。遇到*时,处理方式无非就是两种:其一,走空转换,*不匹配任何字符;其二,*匹配若干字符后走空转换。因此,对于*的处理,可以得到如下算法:
1.遇到*时,默认走空转换,此时,记录待匹配字符在str中的位置为index,进入“尝试阶段”,若尝试失败,会需要回到该位置。
2.继续读取字符,进行状态转换,若发现输入的字符不匹配任何转换,则说明之前对*的处理不正确,尝试失败。于是回到尝试前的状态:待处理字符仍为str[index],此时,在*的状态转换图中,选择由body接收一个字符转换到body,然后进行空转换。也就是尝试用*只匹配一个字符,并更新index。
3.不断地重复步骤2,直到遇到新的*或者字符串末尾,表示对之前的*处理成功。若遇到新的*,则回到步骤1;
以上算法,每次尝试失败后,*的匹配量增加一个字符,不断地进行尝试。为什么遇到新的*就表示之前的*已经成功匹配了呢?前者难道不能匹配更多的字符?因为倘若前者能匹配更多的字符,也可以将其交由后者匹配掉。采用最小原则即可。
既然方法如此简单,可以舍弃生成节点方式,直接在原字符串上面进行状态转移,将字符视为状态即可。用p_ptn表示当前状态,用p_str表示待匹配的字符。p_saved_ptn表示正在尝试匹配的*,而p_saved_str表示开始尝试时最前的未匹配的字符。
public boolean isMatch(String str, String ptn) {
int p_str = 0; // index of current input str
int p_ptn = 0; // index of current pattern
int p_saved_str = -1; // index of latest unmatched str
int p_saved_ptn = -1; // index of latest unmatched star
while (p_str < str.length()) {
char s = str.charAt(p_str);
char p = p_ptn < ptn.length() ? ptn.charAt(p_ptn) : 0;
if (s == p || p == '?') {
p_str++;
p_ptn++;
} else if (p == '*') {
p_saved_ptn = p_ptn++;
p_saved_str = p_str;
} else if (p_saved_ptn >= 0) {
p_ptn = p_saved_ptn + 1;
p_str = ++p_saved_str; // '*' matches another char
} else {
return false; // characters do not match; p_ptn >= ptn.length() and there is no saved_ptn
}
}
while (p_ptn < ptn.length()) {
if (ptn.charAt(p_ptn++) != '*') return false;
}
return true;
}
源码见044_Wildcard_Matching_2.java
3. 动态规划
记dp[i][j]表示pattern前i位是否能匹配str前j位。那么有dp[i][j]=:
- dp[i-1][j-1], if ptn[i-1]==str[j-1] or ptn[i-1]=='?'
- dp[i-1][j] || dp[i-1][j-1] || dp[i-1][j-2] || ... || dp[i-1][0], if ptn[i-1]=='*', 即:
- dp[i-1][j] || dp[i][j-1]
- false, 其它情况
注意ptn[i-1]表示ptn的第i位
只需求出i=0以及j=0的情况下dp的值,然后根据上式求出整个dp
public boolean isMatch(String str, String ptn) {
boolean[][] dp = new boolean[ptn.length() + 1][str.length() + 1];
dp[0][0] = true;
for (int i = 1; i <= ptn.length(); i++) {
dp[i][0] = dp[i - 1][0] && ptn.charAt(i - 1) == '*';
}
// for (int j = 1; j <= str.length(); j++) {
// dp[0][j] = false;
// }
for (int i = 1; i <= ptn.length(); i++) {
for (int j = 1; j <= str.length(); j++) {
dp[i][j] = ((ptn.charAt(i - 1) == str.charAt(j - 1) || ptn.charAt(i - 1) == '?') && dp[i - 1][j - 1]) ||
(ptn.charAt(i - 1) == '*' && (dp[i - 1][j] || dp[i][j - 1]));
}
}
return dp[ptn.length()][str.length()];
}